Benchmarks
Benchmark # 01 =================================
Single thin rectangular tape, width: 12 mm, thickness: 1 μm, Ic=300 A, frequency=50 Hz
Simulations:
- I/Ic=0.5 to study J and By profiles along the width of the tape (halfway across the thickness, i.e. from x=-6 mm to x=6 mm, y=0)
- I/Ic=0.1, 0.2,…,0.9 to compute the AC loss.
Benchmark # 02 =================================
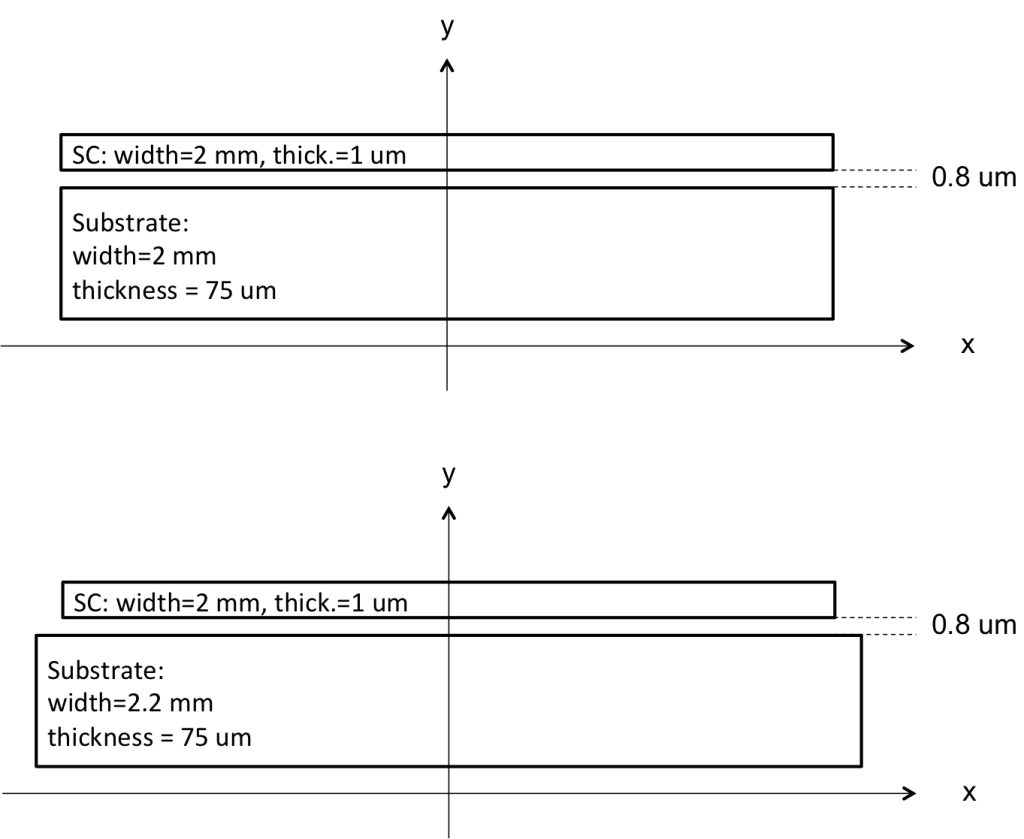
One thin rectangular superconductor with magnetic substrate in applied perpendicular field.
HTS width: 2 mm, HTS thickness: 1 μm, Ic=50 A, substrate width= 2 mm or 2.2 mm, substrate thickness=75 μm, separation between HTS and substrate (distance between the top of the substrate and the bottom of the HTS): 0.8 μm, magnetic permeability of the substrate: μr=100 (linear, isotropic), Frequency of the applied field: 50 Hz, amplitude of the applied field: from 1 to 20 mT (suggested values: 1,2,5,10,20).
Simulations (e.g. at 20 mT):
- J and B profiles in the individual tapes (see previous benchmark)
- AC loss in HTS
Benchmark # 03 =================================
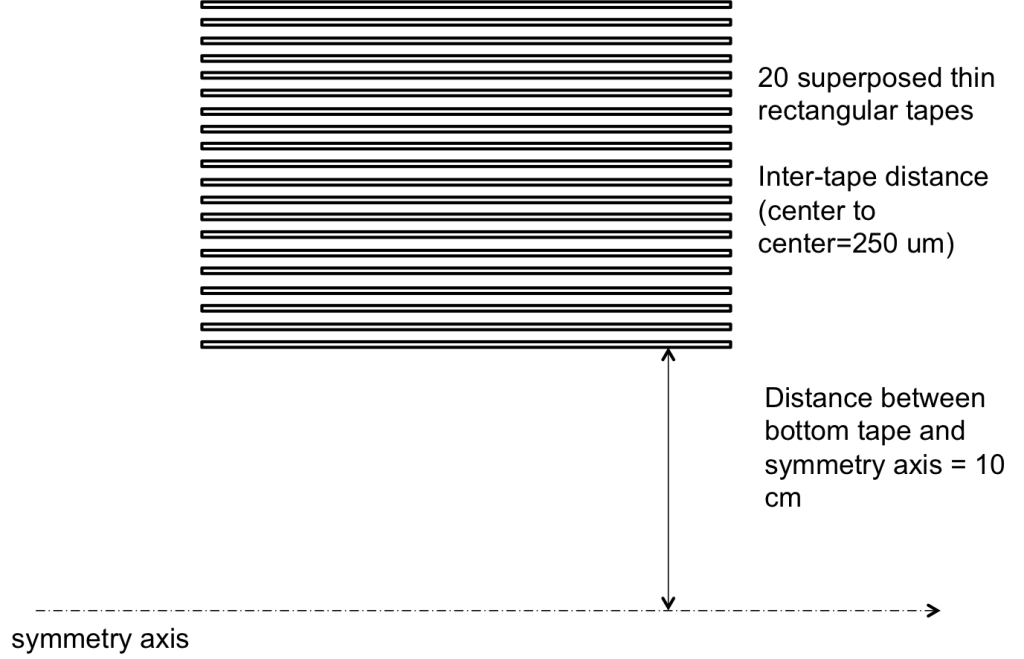
Twenty superposed thin tapes representative of the cross-section of a racetrack coil. Tapes are connected in series. A symmetry plane is defined to take into account the presence of the other part of the coil. Tape width: 12 mm Ic=300 A. Distance between HTS tapes (center-to-center for each HTS film): 250 μm. Distance between inner tape and symmetry plane: 10 cm Frequency=50 Hz
Simulations:
- I/Ic=0.5 to study J and B profiles in the individual tapes
- I/Ic=0.1, 0.2,…,0.9 to compute the AC loss
Benchmark # 04 =================================
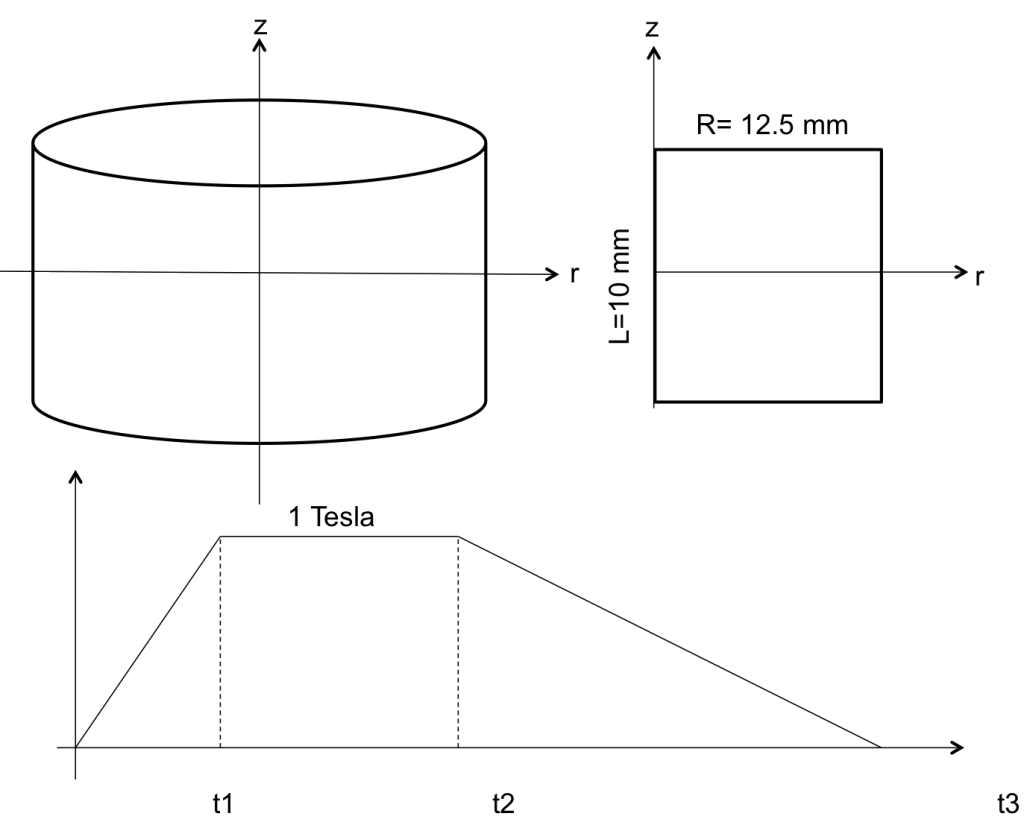
A superconducting bulk cylinder subjected to magnetization. With the use of an axis-symmetric model the geometry can be reduced to 2-D Cylinder’s radius: R=12.5 mm Cylinder’s height: L=10 mm Jc=3·10^8 A/m^2, [t1,t2,t3]=[ 5,10,15] s, magnetic field ramp: as displayed at the bottom of the figure below (Bmax=1 T)
Compare J distributions and magnetization at t1, t2, t3; Bz profiles 2 mm above surface, dissipation.
Benchmark # 05 =================================
A superconducting bulk cube subjected to magnetization, to be simulated in 3-D.
Bulk side: 10 mm, Jc=10^8 A/m^2. In case power-law is used: n=100. The cube is subjected to a sinusoidal magnetic field in the z direction: amplitude=200 mT, frequency=50 Hz.
Compare J distributions at the cross-sections: Jy at y=5 mm, Jz at y=0.12 mm and z=1.1 mm, |J| at z=0.12 mm and z= 5 mm.
Compare also initial magnetization curve M(H) from t=0 s to the first peak (t=0.005 s).
Benchmark # 06 =================================
The high-temperature superconducting (HTS) dynamo benchmark problem consists of a permanent magnet rotating past a stationary HTS wire in the open-circuit configuration and assumes for simplicity the 2D (infinitely long) case. The geometry of the problem is shown below.
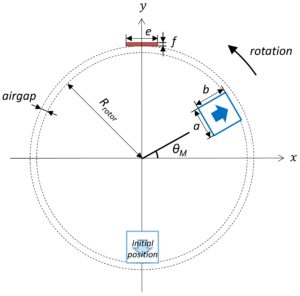
The PM has a width a and height b and a remanent flux density Br. The initial position of the PM is such that the centre of its outer face is located at (0, –Rrotor), i.e., θM(t = 0) = –π/2. The HTS wire has a width e and thickness f and is positioned such that its inner face is located (0, Rrotor + airgap). Table I lists the assumed parameters for the model. Only the superconducting layer of the HTS wire is modelled and Jc is assumed to be constant (where Jc = Ic/(e·f)).
More details, including voltage definitions and the expected results, are provided here. Data can be downloaded at the University of Cambridge data repository (here).